Nueva teoría profundiza sobre la creación de patrones de Turing en biología
Científicos del EMBL llevan la teoría de Turing un paso más allá, ayudando a entender cómo se forman patrones biológicos
Investigadores del grupo de James Sharpe en el Laboratorio Europeo de biología Molecular (EMBL) han ampliado la teoría original de Alan Turing sobre cómo se crean patrones en sistemas biológicos. Este nuevo modelo teórico, que en parte se llevó a cabo en el Centro de Regulación Genómica (CRG), puede dilucidar si los patrones que encontramos en la naturaleza se rigen por el modelo matemático de Turing y podría tener aplicaciones en ingeniería de tejidos. Sus resultados se publican en Physical Review X.
EMBL scientists extend Turing's theory to help understand how biological patterns are created.
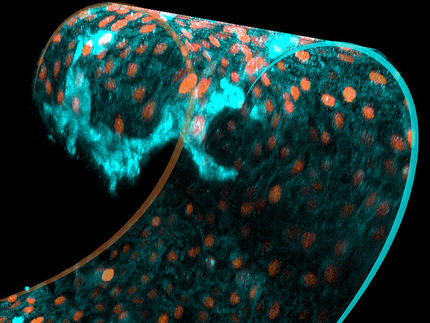
Xavier Diego, EMBL.
Alan Turing trató de explicar cómo surgen patrones en la naturaleza con su teoría sobre la morfogénesis en 1952. Turing propuso que tanto las rayas de una cebra, como la disposición de los dedos o la espiral que dibujan las semillas de un girasol, están determinadas a través de una interacción entre moléculas que se extienden a través del espacio e interactúan químicamente entre sí. La famosa teoría de Turing se puede aplicar a diversos campos, de la astrofísica a la biología.
Se ha propuesto que muchos patrones biológicos surgen según las reglas de Turing, pero los científicos aún no han sido capaces de proporcionar una prueba definitiva sobre si estos patrones biológicos se rigen por el modelo de difusión y reacción propuesto por Turing. El análisis teórico también parecía predecir que los sistemas de Turing son intrínsecamente muy frágiles, algo poco probable para un mecanismo que gobierna la formación de patrones en la naturaleza.
Más allá de la teoría de Turing
Xavier Diego, James Sharpe y colegas de la nueva sede del EMBL en Barcelona analizaron pruebas computacionales y observaron que los sistemas de Turing pueden ser mucho más flexibles de lo que se pensaba. Siguiendo este indicio, los científicos, en aquel momento en el CRG y ahora en EMBL Barcelona, han ampliado la teoría original de Turing utilizando la teoría de grafos: una rama de las matemáticas que estudia las propiedades de las redes y que facilita el trabajo con sistemas complejos y realistas. Esto les llevó a entender que la topología de red - la estructura de retroalimentación entre los componentes en una red - es lo que determina muchas propiedades fundamentales de un sistema de Turing. La nueva teoría topológica proporciona una visión unificadora de muchas propiedades cruciales para los sistemas de Turing que antes no se entendían bien y define explícitamente qué se requiere para hacer un sistema de Turing exitoso.
Un sistema de Turing consiste en un activador que se difunde con una tasa mucho menor que un inhibidor, y que de este modo da lugar a un patrón. La mayoría de modelos de Turing requieren un ajuste preciso de los parámetros. La necesidad de este ajuste tan preciso es justamente lo que impide que los modelos definidos hasta ahora puedan ser lo suficientemente robustos como para que reflejen auténticos procesos de formación de patrones. "Hemos aprendido que estudiar sistemas de Turing a través de la lente topológica simplifica su análisis. Por ejemplo, entender el origen de las restricciones en el caso de la difusión se vuelve más intuitivo, y aún más importante, ahora es mas fácil ver qué modificaciones son necesarias para relajar estas restricciones", explica Xavier Diego, autor principal del artículo.
"Nuestro enfoque se puede aplicar a diferentes sistemas de Turing, y las propiedades de esos sistemas serán ciertas para redes con cualquier número de componentes. Ahora podemos predecir si la actividad en dos nodos de la red está sincronizada o no, y también sabemos qué modificaciones son necesarias para cambiarla. Esto nos permite construir redes que superpongan en el espacio a cualquier par de sustancias que queramos , lo que podría tener aplicaciones muy interesantes en ingeniería de tejidos".
Jeroglíficos de Turing para investigación experimental
Los investigadores también proporcionan un método gráfico y visual que permite analizar con facilidad redes existentes o crear nuevos diseños. "En el laboratorio los llamamos jeroglíficos de Turing", dice James Sharpe, jefe del grupo de investigación de EMBL Barcelona que ha liderado el trabajo. "Esperamos que tanto científicos teóricos como experimentales utilicen nuestros hallazgos y jeroglíficos para intentar implementar redes de Turing en células biológicas".
Esta nueva teoría proporciona a grupos de investigación experimentales un nuevo enfoque para hacer que células biológicas desarrollen patrones en el laboratorio. Si los grupos experimentales lo llevan a cabo con éxito, las preguntas sobre si la teoría de la morfogénesis de Turing es aplicable a sistemas biológicos tendrán finalmente respuesta.
Publicación original
Más noticias del departamento ciencias
Reciba la industria de las ciencias biológicas en su bandeja de entrada
No se pierda nada a partir de ahora: Nuestro boletín electrónico de biotecnología, productos farmacéuticos y ciencias de la vida le pone al día todos los martes y jueves. Las últimas noticias del sector, los productos más destacados y las innovaciones, de forma compacta y fácil de entender en su bandeja de entrada. Investigado por nosotros para que usted no tenga que hacerlo.
