Nuevo modelo que muestra la propagación de enfermedades infecciosas
Las simulaciones muestran que las tasas de infección de COVID-19 muestran una marcada disminución que es resultado del distanciamiento social
Los físicos de la Universidad de Münster han demostrado en simulaciones de modelos que las tasas de infección por COVID-19 disminuyen significativamente a través del distanciamiento social. Para ello, combinaron la teoría funcional de la densidad dinámica para describir las partículas que interactúan y el modelo SIR, una teoría para describir la propagación de las enfermedades infecciosas.
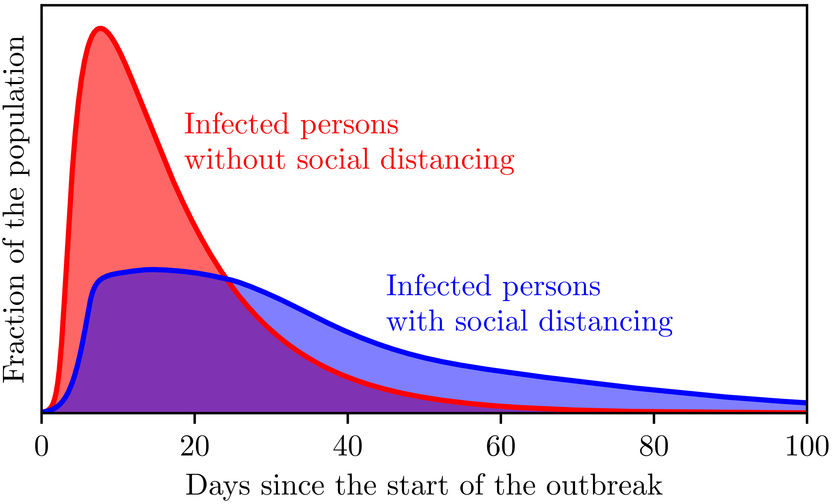
Las simulaciones basadas en un nuevo modelo de propagación de epidemias muestran la disminución de las tasas de infección como resultado del distanciamiento social.
M. te Vrugt et al./Nature Research
Los científicos de todo el mundo han estado trabajando a fondo en la investigación de las enfermedades infecciosas tras el brote mundial de la enfermedad COVID-19, causada por el nuevo coronavirus SARS-CoV-2. Esto concierne no sólo a los virólogos, sino también a los físicos, que están desarrollando modelos matemáticos para describir la propagación de las epidemias. Tales modelos son importantes para probar los efectos de varias medidas diseñadas para contener la enfermedad, como las máscaras faciales, el cierre de edificios públicos y empresas, y la conocida de distanciamiento social. Estos modelos sirven a menudo como base para decisiones políticas y subrayan la justificación de cualquier medida adoptada.
Los físicos Michael te Vrugt, Jens Bickmann y el Prof. Raphael Wittkowski del Instituto de Física Teórica y el Centro de Nanociencia Suave de la Universidad de Münster han desarrollado un nuevo modelo que muestra la propagación de las enfermedades infecciosas. El grupo de trabajo dirigido por Raphael Wittkowski está estudiando la Física Estadística, es decir, la descripción de sistemas que consisten en un gran número de partículas. En su trabajo, los físicos también utilizan la teoría funcional de la densidad dinámica (DDFT), un método desarrollado en la década de 1990 que permite describir las partículas que interactúan.
Al principio de la pandemia de la corona, se dieron cuenta de que el mismo método es útil para describir la propagación de las enfermedades. "En principio, las personas que observan el distanciamiento social pueden ser modeladas como partículas que se repelen entre sí porque tienen, por ejemplo, la misma carga eléctrica", explica el autor principal Michael te Vrugt. "Así que tal vez las teorías que describen las partículas que se repelen entre sí podrían ser aplicables a las personas que mantienen su distancia entre sí", añade. Basándose en esta idea, desarrollaron el llamado modelo SIR-DDFT, que combina el modelo SIR (una conocida teoría que describe la propagación de enfermedades infecciosas) con el DDFT. La teoría resultante describe a las personas que pueden infectarse entre sí pero que mantienen su distancia. "La teoría también permite describir los puntos calientes con personas infectadas, lo que mejora nuestra comprensión de la dinámica de los llamados eventos de súper propagación a principios de este año, como las celebraciones de carnaval en Heinsberg o el après-ski en Ischgl", añade el coautor Jens Bickmann. Los resultados del estudio han sido publicados en la revista "Nature Communications".
El grado de distanciamiento social que se practica se define entonces por la fuerza de las interacciones repulsivas. "Como resultado", explica Raphael Wittkowski, el líder del estudio, "esta teoría también puede utilizarse para probar los efectos del distanciamiento social simulando una epidemia y variando los valores de los parámetros que definen la fuerza de las interacciones". Las simulaciones muestran que las tasas de infección muestran de hecho una marcada disminución que es resultado del distanciamiento social. El modelo reproduce así el conocido efecto de "aplanamiento de la curva", en el que la curva que representa la evolución del número de personas infectadas a lo largo del tiempo se hace mucho más plana como resultado del distanciamiento social. En comparación con las teorías existentes, el nuevo modelo tiene la ventaja de que los efectos de las interacciones sociales pueden modelarse explícitamente.
Nota: Este artículo ha sido traducido utilizando un sistema informático sin intervención humana. LUMITOS ofrece estas traducciones automáticas para presentar una gama más amplia de noticias de actualidad. Como este artículo ha sido traducido con traducción automática, es posible que contenga errores de vocabulario, sintaxis o gramática. El artículo original en Inglés se puede encontrar aquí.
Publicación original
Más noticias del departamento ciencias
Reciba la industria de las ciencias biológicas en su bandeja de entrada
No se pierda nada a partir de ahora: Nuestro boletín electrónico de biotecnología, productos farmacéuticos y ciencias de la vida le pone al día todos los martes y jueves. Las últimas noticias del sector, los productos más destacados y las innovaciones, de forma compacta y fácil de entender en su bandeja de entrada. Investigado por nosotros para que usted no tenga que hacerlo.
